Changes in interest rates have an impact on the value of stock options that shouldn’t be overlooked.
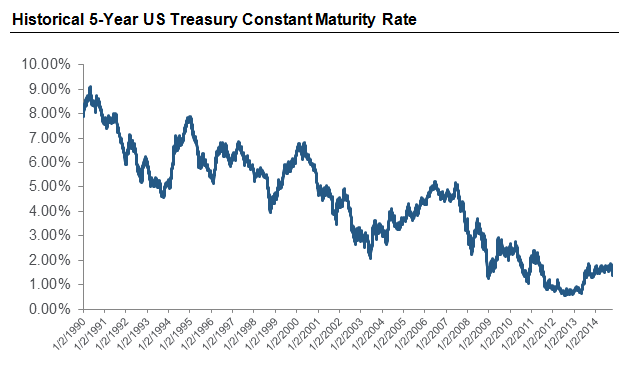
The rates of return for US Treasury Bills, known as "risk-free rates," have been significantly lower for the period since the
2008-09 Recession than for any extended time in recent history. This sharp decline in risk-free rates of return was partially a result of the Federal Reserve keeping the overnight borrowing rate low in an effort to promote investment in equity markets.
The prevailing wisdom is that interest rates will rebound towards historical norms as the market continues to recover. Although the timing of this rally remains unclear, it is important to understand the effects that the inevitable increase in risk-free rates will have on equity compensation valuations.
Impact of Risk-Free Rate on Stock Options
To determine the impact of risk-free rates on a Black-Scholes fair value— the most popular model for valuing stock options— it is first necessary to understand the role of the interest rate within the formula. Black-Scholes fair value requires six inputs:
- Stock price on date of grant
- Strike price (or exercise price)
- Risk-free rate
- Expected volatility
- Expected life
- Dividend yield
The difference between the risk-free rate and the dividend yield is called the "drift rate." This is synonymous with the long-term growth rate (or decay rate, if the dividend yield is greater than the risk-free rate) of a given security. For example, if the risk-free rate is 3% and a stock’s dividend yield is 1%, that stock would be expected to grow, on average, 2% per year, according to the Black-Scholes formula.
As an example, we will use an "at-the-money" stock option with a grant and strike price of $100.00, an expected volatility of 40%, an expected lifespan of 6.00 years, and a 0% dividend yield. Increasing the risk-free rate from 0.50% to 5.50% at 50 basis point increments yields the following increase in fair value:
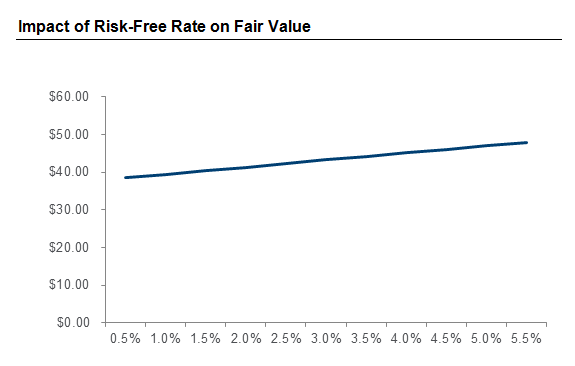
As you can see, as the risk-free rate increases so does the fair value of the stock options. For our example outlined above, this linear equation has a slope of 1.90. In other words, for every 1% the risk-free rate increases, the fair value increases by 1.9%.
The following table shows a rule of thumb estimate for the percentage increase in fair value for each 1.00% increase in risk-free rate, given a particular volatility and expected life.
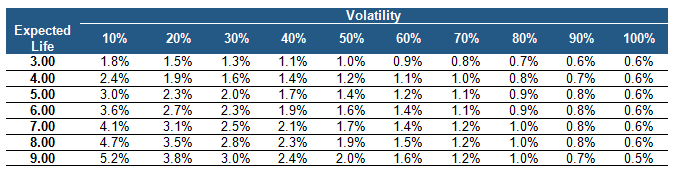
However, for a more complete and nuanced answer to our question of how risk-free rate increases impact the fair value of stock options, we need to look at the relationship between changes in the other five inputs of the Black-Scholes formula.
Volatility: Changes in the risk-free rate will have a varying degree of impact on fair value depending on the company’s volatility. As illustrated in the chart below, the lower the volatility, the greater impact the risk-free rate will have on fair value. At a volatility of 10%, the linear equation has a slope of 3.59— almost twice the slope of the baseline case— while the slope decreases to 0.62 at 100% volatility.
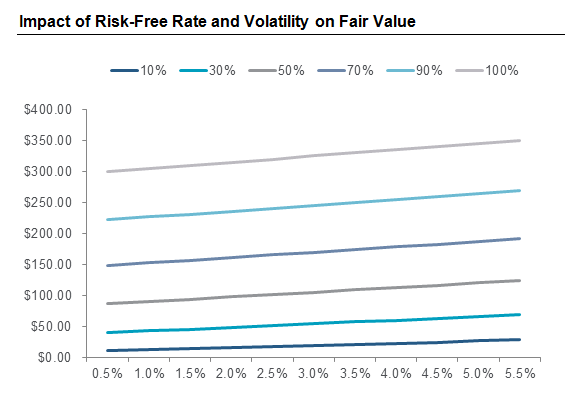
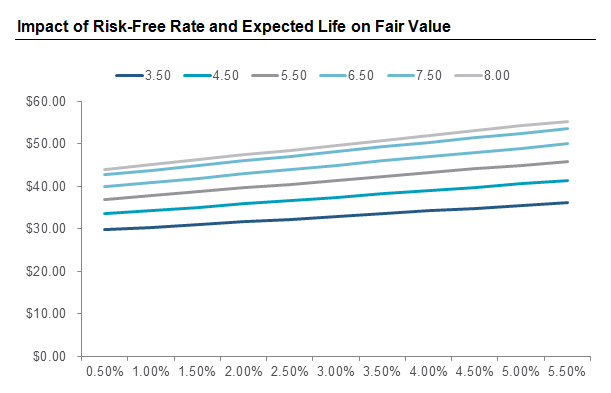
Expected Life: The relationship between fair value and the risk-free rate is also influenced by changes in the expected life of the stock option. Converse to volatility, the impact on fair value is greater when the expected life increases. Over a longer expected life, the long-term drift rate becomes more important relative to the other inputs such as volatility. The slope of the linear equation increases to 2.27 as expected life increases to eight years, and falls to 1.28 at an expected life of 3.50 years.
S/K Ratio: The ratio of strike price to grant price (often referred to as the S/K ratio) has a large effect on fair value. However, the risk-free rate affects fair value comparably under different S/K ratios. It should be noted that a large majority of options are granted with the strike price equal to the grant price, and the need for valuations at other S/K ratios would be low.
Dividend Yield: As with the S/K ratio, the risk-free rate’s impact on fair value is similar regardless of dividend yield.
Next Steps
While the risk-free rate is not a significant driver in a Black-Scholes valuation, it does play a role. Companies should be aware that the risk-free rate is expected to rise in the near future, and that this increase will result in slightly higher valuations for stock options. Companies that wish to mitigate this increase should reference our paper, "Using Capped Options to Collar Volatility," for option design considerations.
To learn more about participating in a Radford survey, please contact our team. To speak with a member of our compensation consulting group, please write to consulting@radford.com.
Related Articles